2021-06-21 Janusz Kapusta
Każdy je ma. To nie oczy, nos, usta czynią człowieka pięknym,
ale odległości pomiędzy, czyli proporcje.
(Janusz Kapusta, Plus Minus, Podręcznik do myślenia, Zysk i S-ka, 2014)
W tym eseju skupię się na zdumiewającym odkryciu, które mi się przytrafiło około 2000 roku w Nowym Jorku i które sprawiło, że piękno stało się – przynajmniej dla mnie – nie tylko nieuchronne, ale i namacalne.
Odkryłem nieznane zasady złotego podziału. W 2003 roku, jako jedyny nie matematyk, byłem zaproszony przez profesora matematyki z New Jersey Institute of Technology Jay Kappraffa i japońskie pismo “Forma” do przedstawienia szeregu swoich odkryć. “Forma” jest oficjalnym periodykiem Towarzystwa Naukowego. Cały numer poświęcony był złotemu podziałowi i naszej najnowszej o nim wiedzy. We wstępie do artykułu, od którego rozpoczynała się prezentacja napisałem:
Ponieważ jestem artystą o zainteresowaniach filozoficznych i matematycznych moje poszukiwania dotyczące złotej proporcji z natury rzeczy musiały się różnić od działań podejmowanych przez matematyków. Na początku głównym powodem mojego zainteresowania się złotą liczbą było jej zadziwiająco częste i zaskakujące występowanie w sztuce, przyrodzie i matematyce. Podświadomie czułem, że coś o takiej mocy i wyjątkowości musi mieć jakieś głębsze podstawy. W 2000 roku odkryłem nieznany wcześniej świat geometrycznych związków istniejących w kwadracie i kole. Była to pierwsza wizualna konstrukcja na świecie łącząca złoty i srebrne proporcje w jednym rysunku. Odkrycie to rozpoczęło moją długą podróż po nieznanej przestrzeni piękna, matematyki i filozofii. Ale to filozofia była przede wszystkim moim powodem i celem poszukiwań. Dla mnie, geometria jest tylko wizualnym językiem dla zrozumienia tego, co widzimy obserwując naturę; pomaga nam zdobyć bardziej całościowe zrozumienie Wszechświata, tak, że potrafimy zobaczyć wszystkie relacje jakby w jednym okamgnieniu.
Można powiedzieć, że źródło mocy złotego podziału wynika z dwóch obszarów, czy działów: po pierwsze – z geometrii, poprzez podział linii w złoty sposób, jaki odkryto w starożytnej Grecji. Uważa się, że znany był już Pitagorasowi, ale pierwszy raz został opisany przez Euklidesa w “Elementach” w IV wieku p.n.e.; po drugie – z liczby, jako stosunku – odkrytego przez Johannesa Keplera – dla dwóch kolejnych wyrazów ciągu Fibonacciego. Stworzyłem trzecie wizualne podejście, w którym złota liczba jest postrzegana jako element większego systemu relacji – geometria i liczba są tkane razem w jednej strukturze wszechświata.
W przytoczonym z artykułu w “Formie” fragmencie chciałbym wytłumaczyć się z jednej rzeczy. Dotyczy – nieskromnego – dopisania siebie do osiągnięć Pitagorasa-Euklidesa i Fibonacciego-Keplera. Chcąc wykorzystać tę wyjątkową sytuację, że artykuł ukazuje się w poważnym matematycznym piśmie chciałem z pełną świadomością napisać, że moje odkrycie jest trzecim w historii złotego podziału, które ma coś dramatycznie nowego i zaskakującego do powiedzenia o najważniejszej proporcji. W matematyce są tylko trzy możliwości oceny czyjejś nowej propozycji: pierwsza – stwierdzenie, że autor się pomylił – trzeba wtedy wykazać błąd w myśleniu lub w obliczeniach; druga – że od kogoś ściągnął – wystarczy więc przedstawić wcześniejsze rozwiązanie; trzecia – która jest następstwem nie znalezienia ani błędu, ani oszustwa – potwierdza, że mamy do czynienia z czymś nowym i wtedy wszyscy muszą ten fakt uznać. Matematycy akceptują dokonania ludzi spoza branży – nie polemizuje się z człowiekiem, który wypowiedział twierdzenie i je udowodnił – ale robią to tylko wtedy, kiedy nie mają innego wyjścia i na pewno nie robią tego z lekkością. Często na konferencjach miałem poczucie intruza, który swoimi odkrywczymi związkami z matematyką czynił im krzywdę. Ich drugi łatwy sposób deprecjacji polega na pomniejszaniu znaczenia odkrycia. Im bardziej ich zaskakuje, tym bardziej udają, że nic się nie zdarzyło. Wiedziałem o tym, doświadczałem tego wcześniej, w związku z tym bardzo pilnowałem, aby moje odkrycie właśnie w ten sposób zostało wyartykułowane. Tak sformułowane zdanie, które się w końcu w druku ukazało, dowodziło czarno na białym, że ani od nikogo nie ściągnąłem, ani tym bardziej, że się pomyliłem.
Lista nazwisk, które odkrywały bogactwo złotej proporcji, aż onieśmiela: Pitagoras, Fidiasz, Platon, Euklides, Witruwiusz, Fibonacci, Piero della Francesca, Leonardo da Vinci, Johannes Kepler, le Corbusier, Roger Penrose. I inni. Wielu innych.
Odkryłem nowe, nieznane, ale przede wszystkim fundamentalne zasady złotego podziału. W konsekwencji te odkrycia udowadniają o wiele głębszą naturę kosmicznego bytu liczby. Brzmi to jak u/z Pitagorasa, który mówił, że liczba jest istotą wszystkich rzeczy i uważał to za swoje najważniejsze spostrzeżenie.
Z tej nowej perspektywy rozumiem więc dlaczego złoty podział był/jest do tej pory jakimś przeoczonym, istniejącym na obrzeżach pojęciem. Niektórzy uważają, że jest jakąś dziwną fantasmagorią – nawet mądrych – ludzi przeszłości. W wielu rzeczach się mylili, dlaczego nie mogli się również mylić z oceną niewymiernej, trudnej do zapamiętania liczby. Sam tego doświadczyłem, kiedy mi się przytrafiła na nowo. Poza tym, że taka proporcja istnieje nie wiedziałem zbyt wiele. Nawet nie pamiętałem jej przybliżonej wartości. Można bez tego żyć? Można. Ale do czasu. Sama liczba wymusi uszanowanie swojego miejsca w kosmosie.
Kiedyś w Nowym Jorku mój kolega artysta, który po paru drinkach poczuł się trochę odważniej zapytał, co ja takiego nowego w tej geometrii odkryłem? Poprosiłem go o kartkę i narysowałem pierwszą zasadę, która mi otworzyła drogę do kolejnych niezwykłych obszarów. Nie uwierzył. Powiedział, „czy to jest możliwe, żeby coś tak fundamentalnie prostego nikt nigdy nie zauważył?”.
Zanim przedstawię ten pierwszy rysunek napiszę parę słów o historycznej powadze złotej proporcji.
PIERWSZE ODKRYCIE
Co to jest proporcja? Proporcja jest równością stosunków. Co to jest stosunek? Stosunek jest – korzystam tu z wprowadzenia do tematu złotej proporcji przez Roberta Lawlora w jego książce „Sacred geometry, Philosophy and practice”; Thames & Hudson, 2003 – porównaniem dwóch różnych wielkości, ilości, jakości lub idei i jest wyrażany wzorem A : B (A do B). Można go też zapisać w postaci ułamka A/B (rys. 1).

rys. 1
Stosunek stanowi więc miarę różnicy, na którą może zareagować przynajmniej jeden z naszych zmysłów. Odróżniamy czerwoną filiżankę od zielonego obrusa tylko dlatego, że nasze nerwy wzrokowe są w stanie wyłapać różnicę częstotliwości emanujących z filiżanki i obrusa. Jak mówił Gregory Bateson, „różnice, które robią różnicę”. Powaga, która wynika z samej nazwy „stosunek” jest widoczna w łacinie i języku angielskim. Słowo „ratio” (stosunek) wywodzi od łacińskiej nazwy „ratio – rozum (jak w słowie „rational” – rozumny, racjonalny).
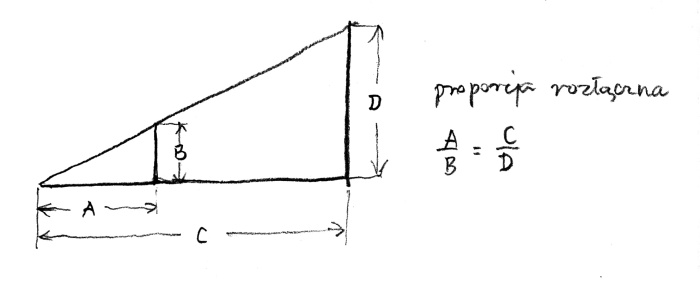
Jeżeli stosunek jest bezpośrednią odpowiedzią na prostą różnicę – proporcja jest znacznie bardziej subtelna i złożona. Składa się z czterech elementów: jeden element ma się tak do drugiego jak trzeci do czwartego. Zapisujemy to: A jest do B jak C jest do D, lub A : B : : C : D, lub A/B = C/D (rys. 2).
rys. 2
Trzeba w tym miejscu jeszcze dodać, że w tak zapisanej proporcji elementy A i D są nazwane skrajnymi, a B i C – środkowymi. Jest to ważne, bo iloczyny wyrazów skrajnych i środkowych są sobie równe: A x D = B x C. Pitagorejczycy nazywali tę procedurę myślenia – nieciągłą, rozłączną proporcją czterech członów.
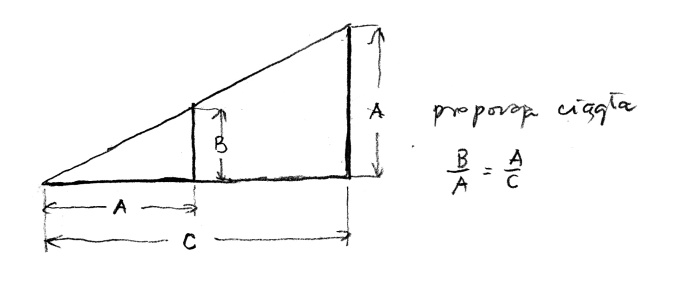
Skoro tak ją nazwali łatwo się domyśleć, że musi istnieć proporcja ciągła składająca się z trzech członów. Jak to jest możliwe – kiedy powiedzieliśmy wcześniej, że proporcja ma zawsze cztery elementy? Po prostu: jeden element ma się tak do drugiego jak drugi do trzeciego. W zapisie: B jest do A jak A jest do C, lub B : A : : A : C, lub B/A = A/C (rys. 3).
rys. 3
To powtórzenie elementu środkowego jest kluczowe. Ponieważ jeżeli teraz pomnożymy wyrazy skrajne i środkowe, czyli B x C i A x A to otrzymamy, że B x C jest równe A² (A do kwadratu). Nasza proporcja staje się nie tylko ciągłą, ale i geometryczną. Ta – ciągła proporcja trzech członów – w myśli greckiej była znana jako analogia. W nauce, prawie i teologii analogia jest jednym z najważniejszych narzędzi, a nawet w teologii najważniejszym. Pozwala to jej na wypowiadanie zdań na temat czwartego członu, który chociaż może być niewiadomy, przecież jest w relacji do pozostałych i z nich organicznie wynika np.: człowiek tak się ma do Boga-człowieka jak Bóg-człowiek do Boga.
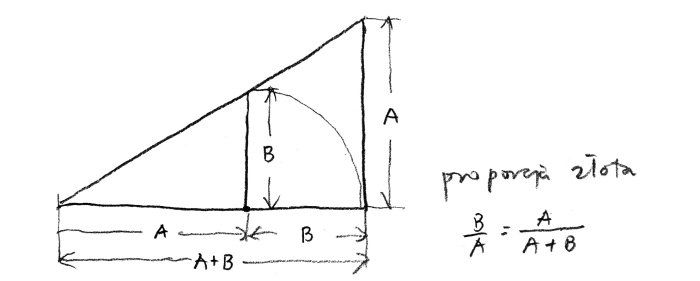
Czy jest możliwa proporcja ciągła składająca się z dwóch członów? Zgadza się – tak. Świat jest pełen cudów i my ludzie czasami je odkrywamy. Istnieje jeden i tylko jeden podział proporcjonalny, który jest możliwy przy użyciu tylko dwóch wyrażeń! Jeden element tak się ma do drugiego jak drugi do sumy ich razem. Zapisujemy to w postaci: B jest do A jak A jest do sumy (A i B), lub B : A : : A : (A+ B), lub B/A = A/(A+B) (rys. 4).
rys. 4
Ta unikalna geometryczna proporcja dwóch elementów otrzymała nazwę „Złotej Proporcji” i jest oznaczana dwudziestą pierwszą literą alfabetu greckiego, Φ (phi). Jej wartość liczbowa jest równa (√5 +1)/ 2 (pierwiastek kwadratowy z 5 plus 1 podzielony przez 2) i wynosi w przybliżeniu 1.618. Odwrotność wynosi (√5 – 1)/2 i jest równa 0.618.
Złoty podział – to podział odcinka na dwie części, większą (A) i mniejszą (B), tak, że część mniejsza (B) ma się tak do większej (A) jak większa (A) do całości (A + B).Nazwa „złoty podział”, „złota proporcja” została wprowadzona dopiero w XIX wieku („A Mathematical History of the Golden Number”, Roger Herz-Fischler, Dover Publications, Inc., 1998). Kiedy Johannes Kepler wypowiadał swoje sławne zdanie na temat złotego podziału oczywiście zamiast o „złotym podziale” odcinka mówił o „stosunku średnim i skrajnym”. Powiedział: „Geometria ma dwa cenne skarby: jeden z nich to Twierdzenie Pitagorasa, drugi – to podział odcinka w stosunku średnim i skrajnym. Pierwszy można porównać do miary złota; drugi możemy nazwać drogocennym klejnotem”. Żeby zrozumieć dlaczego na początku XVI wieku Luca Pacioli w swojej książce – którą ilustrował Leonardo da Vinci – nazwał złoty podział już nie tylko drogocennym klejnotem, ale „boską proporcją” (książka nazywała się „De divina proportione”), musimy posunąć nasze pytanie o ilości elementów występujących w złotej proporcji o jeden – boski – krok dalej.
Czy jest możliwy taki zapis złotej proporcji w której występuje tylko jeden wyraz? W książce „Boska proporcja”, którą Pacioli zadedykował Ludwikowi Sforzy podał pięć powodów dlaczego nazwał ją boską. Pierwszym, najważniejszym powodem było, że „Bóg jest tylko jeden”. Pacioli porównuje wyjątkową wartość złotej proporcji do faktu, że jedność „jest najwyższym określeniem samego Boga”. Żeby ujawnić tę tajemnicę złotej proporcji zmodyfikujemy nieco poprzedni rysunek (rys. 5).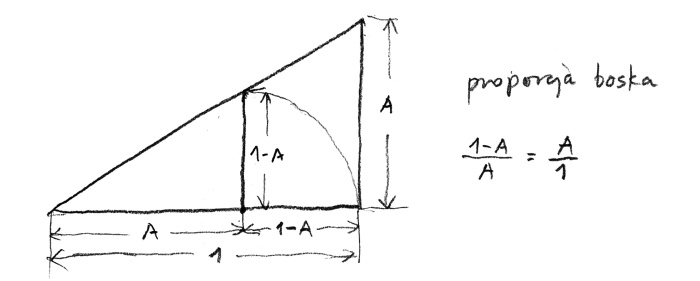
rys. 5
Przyjmiemy, że odcinek, który chcemy podzielić ma wartość jeden. Kiedy część większą oznaczymy przez A, wtedy część mniejszą możemy oznaczyć 1 – A (jeden minus A). Postępując zgodnie z wcześniej przyjętymi zasadami możemy napisać: (1 – A) tak się ma do A, jak A do 1, lub (1 –A) : A :: A : 1, albo (1 – A)/A = A/1. Jeżeli – jak to robiliśmy wcześniej – pomnożymy wyrazy skrajne i środkowe otrzymamy równość: (1 – A) x 1 = A x A. Występuje tu tylko jeden element! Czy to nie jest boskie?
DRUGIE ODKRYCIE
Johannes Kepler (1571 – 1630) miał powody, żeby do złotej liczby mieć stosunek szczególny. Odkrył nieznaną do niej drogę i nie była to droga geometrii. Inicjujące wydarzenie miało miejsce cztery wieki wcześniej. W 1202 roku Leonardo Fibonacci (1170 – 1250) – włoski matematyk – napisał książkę „Liber Abaci”, w której pierwszy raz w Europie przekonująco uzasadnił przewagę cyfr indyjsko-arabskich nad cyframi rzymskimi. W pewnym fragmencie książki zadał zagadkę dotyczącą rozmnażania się królików. Na początku jest tylko jedna młoda para – samiec i samica. Po miesiącu ta para dorasta i może spłodzić następną parę. W trzecim więc miesiącu na scenie mamy dwie pary: rodziców i dzieci. Zgodnie z regułami – para dzieci musi czekać jeden miesiąc, żeby dorosnąć, a rodzice mogą wydawać na świat następną parę. Pytanie Fibonacciego było – ile par królików pojawi się na świecie po 12 miesiącach. W historii matematyki odpowiedź na tę prostą zagadkę jest niezwykle ważna. Doprowadziła do ciągu znanego od XIX wieku jako ciąg Fibonacciego. Zaczyna się od dwóch jedynek i zawsze dodaje się dwie ostatnie liczby, żeby powstała kolejna. Na początku – „ostatnimi liczbami” – są właśnie jedynki. 1 dodać 1 równa się 2; 2 dodać 1 równa się 3; 3 dodać 2 równa się 5. A potem kolejno: 8, 13, 21, 34, 55, 89. 144 jest dwunastą liczbą ciągu i odpowiedzią na zagadkę Fibonacciego. Niezwykłość Keplera polegała na tym, że podzielił przedostatni wyraz ciągu, czyli „89” przez „144” i dostał w wyniku liczbę 0,618 – przybliżoną wartość złotej liczby. To było sensacyjne. Im bardziej ciąg się wydłuża, tym wartość ilorazu dwóch sąsiednich liczb zbliża się do złotej liczby. Nie tylko geometryczny podział, ale i ciąg liczbowy zmierzają w to samo miejsce! A to już nie mogło być przypadkowe. Wiek XIX potraktował odkrycie Keplera z należytą powagą. Liczby ciągu Fibonacciego zaczęły pojawiać się wszędzie: w zjawiskach fizycznych, biologicznych, astronomicznych, artystycznych, a nawet finansowych.
Nie czas tu i miejsce na ujawnienie bogactwa wynikającego z tych dwóch metod docierania do złotego podziału bądź geometrycznie, bądź liczbowo. Jest do prześledzenia bardzo bogata literatura i to zarówno w formie książkowej jak i elektronicznej.
TRZECIE ODKRYCIE
U podłoża mojego odkrycia złotej proporcji leżały dwa spostrzeżenia: jedno natury filozoficznej, drugie – estetycznej. Zacznijmy od estetycznej. W każdym wprowadzeniu do złotego cięcia mówi się, że jest to podział odcinka na dwie części tak, by stosunek długości krótszej z nich do dłuższej był taki sam, jak części dłuższej do całego odcinka. Nie podobało mi się, że stosunek ten jest zawsze zaznaczony na diagramie jako podróż dookoła dzielonego odcinka (rys. 6a).
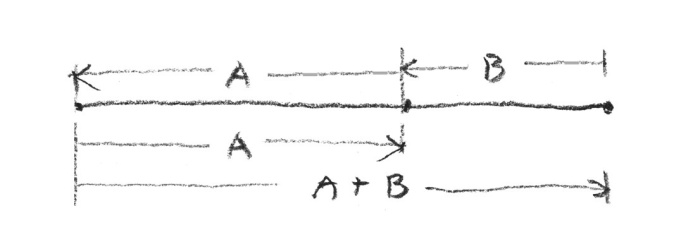
rys. 6a
Ujawniała proporcję, ale nie ciągłość. Wydawało mi się, że będzie bardziej adekwatne i mądre wykorzystanie średnicy w kole – jest równa dwóm promieniom. Wystarczyło jeden z nich podzielić w złotym podziale, żeby proporcja przestawała była statyczna i ujawniała się nagle w swojej nieskończonej możliwości rozwoju: i do wielkości, i do małości (rys. 6b).
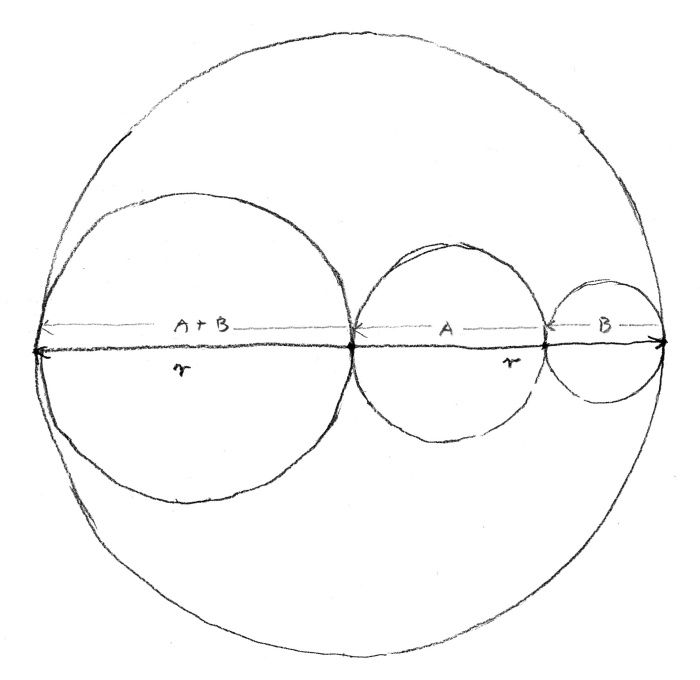
rys. 6b
Drugie spostrzeżenie była bardziej zasadnicze. Znałem je poniekąd ze wspomnianej książki Roberta Lawlora „Sacred Geometry” i z książki„ „Tajemnicza formuła Boga” Petera Plichty. W odróżnieniu od znanego układu współrzędnych kartezjańskich, kiedy po dwóch stronach osi przechodzącej przez punkt zero symetrycznie są położone ciągi liczb dodatnich i liczb ujemnych, Lawlor przedstawił egipski ciąg liczbowy, który zaczynał się od jeden. Po jego prawej stronie ciągnęły się w nieskończoność liczby naturalne, a po lewej od jeden – liczby ułamkowe, które są odwrotnością liczb całkowitych prawej strony. Uświadomiłem sobie, że jeżeli narysujemy tę prawidłowość na osi liczbowej zaczynając od zera i nanosząc liczby całkowite i ich odwrotności (rys. 7), wtedy – obojętnie jak wielką i w jakiej odległości od jeden liczbę przyjmiemy – zmieści się ona pomiędzy jeden i zero; dla miliona będzie to jedna milionowa – bardzo blisko zera – ale ciągle w przedziale zero – jeden (patrz rysunek).
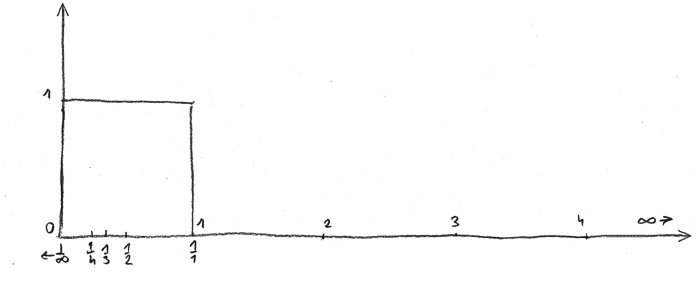
rys. 7
Narysowałem kwadrat. Jeżeli go położyć na płaszczyźnie nieskończonego Wszechświata – to wtedy każdy punkt tego Wszechświata zmieści się poprzez swoją odwrotność – jak w oku człowieka – w narysowanym kwadracie. Dla mnie to było wstrząsające. Znalazłem jak Borges swój punkt Alef.
Co narysowałam zaprzyjaźnionemu artyście w Nowym Jorku? Na początku narysowałem kwadrat (rys. 8).
rys. 8
Jeden kwadrat jest ważny. Od niego zaczyna się rzeczywistość i realność. Zawsze jeżeli coś jest – jest jedno. Wszystkie kwadraty zaczynają się od pierwszego. Kiedy nie ma jednego – nie ma nie tylko kwadratu, ale nie ma nic (po angielsku – jest nic – it’s nothing). Na pamiątkę Pitagorasa przyjąłem dziesięć kwadratów (rys. 9).
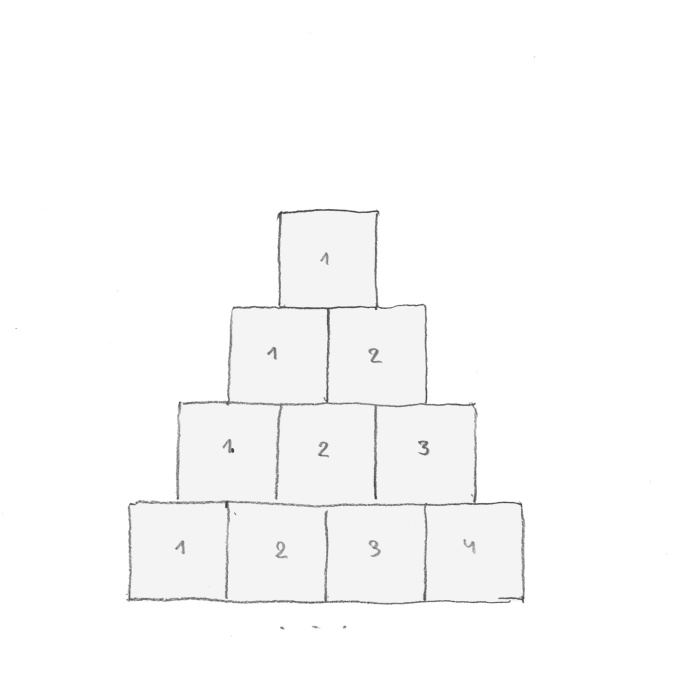
rys. 9
Dziesięć (1 + 2 + 3 + 4 = 10) było dla niego liczbą świętą i doskonałą. Ułożyłem piramidę (tetraktys) nie z punktów – jak zrobili to pitagorejczycy – ale z kwadratów.
Poprowadziłem styczne do kwadratów (rys. 10).
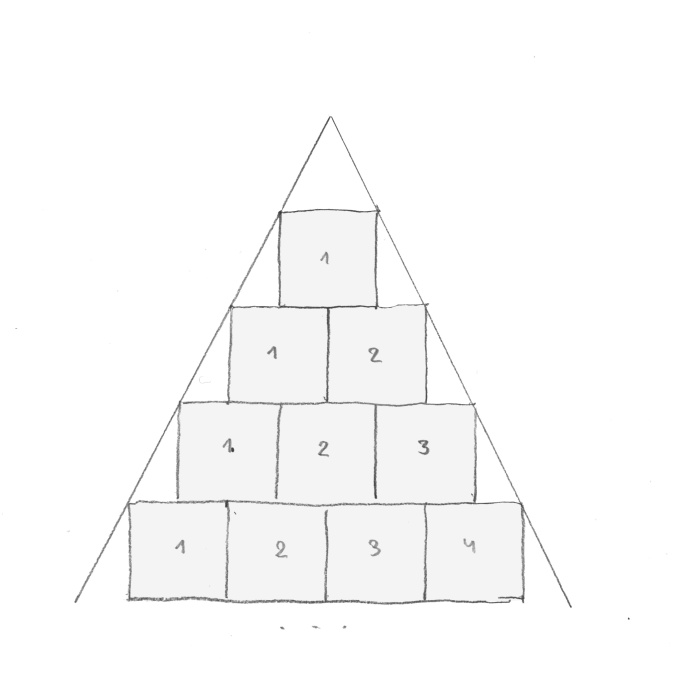
rys. 10
Styczne spotykają się w pustce ponad kwadratem jeden. Przed chwilą mówiłem, że w realnym świecie wszystko zaczyna się od jeden. Gdzie się więc styczne spotykają? Nazwałem pierwszy kwadrat „realnym”, a wtedy nieistniejący kwadrat ponad nim, w którym zbiegają się styczne, nazwałem „wirtualnym”, „duchowym” (rys. 11).
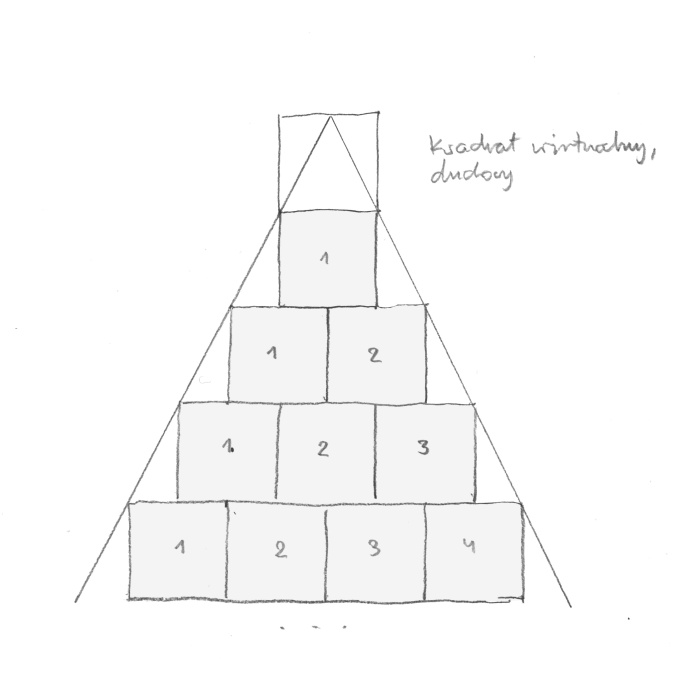
rys. 11
W następnym kroku wpisałem w kwadraty koła i poprowadziłem do nich styczne (rys. 12).
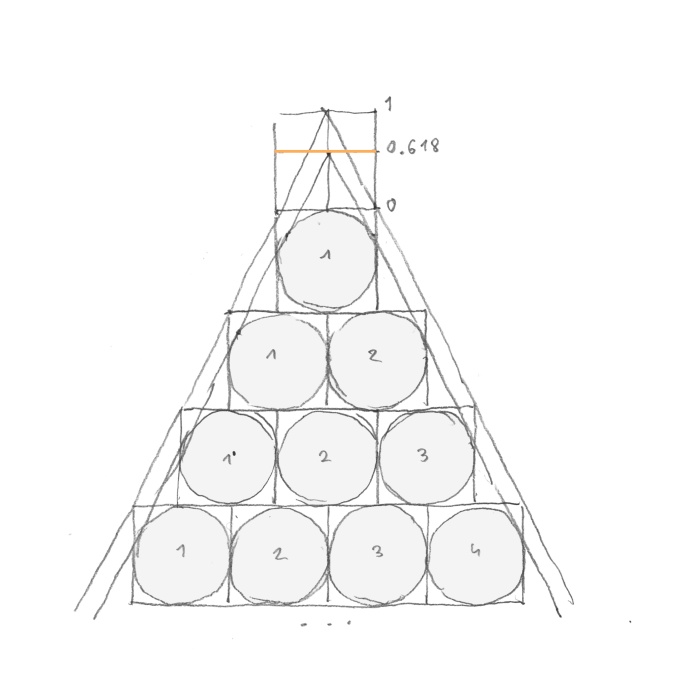
rys. 12
Wtedy wydarzył się cud. Okazało się, że styczne do kół są przesunięte względem stycznych do kwadratu w złotym podziale! Kwadrat i koło to dwie najważniejsze figury naszego Wszechświata. „Czy to jest możliwe, żeby coś tak fundamentalnie prostego nikt nigdy nie zauważył?” – jak pamiętacie – powiedział mój kolega.
Nikt nigdy nie zauważył ich Boskiego związku.
Skoncentrowałem się na nowo powstałym wirtualno-duchowym kwadracie. Niby go nie ma, a jak ważne wydarzenia się w nim ujawniają (rys. 13).
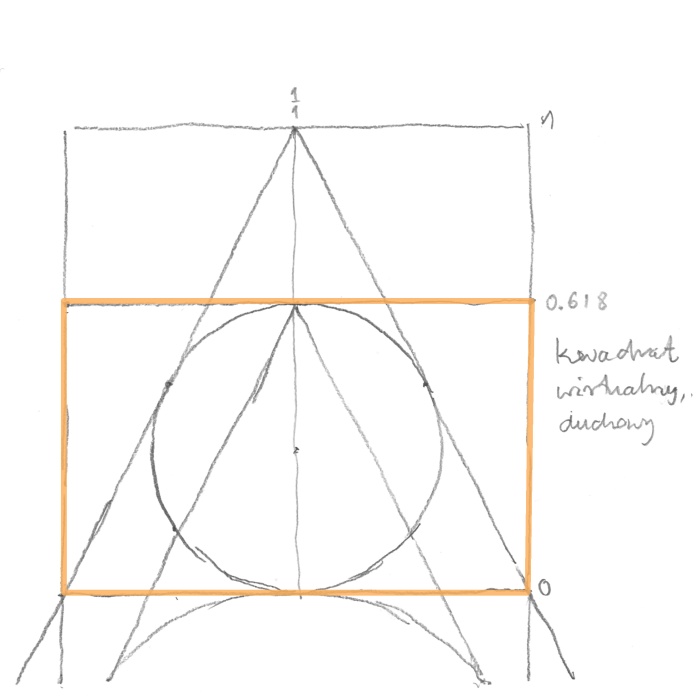
rys. 13
Jeżeli przez punkt, w którym zbiegają się proste styczne do kół poprowadzić prostą równoległą do podstawy wirtualnego kwadratu – utworzy ona złoty prostokąt. Kiedy wpisałem w ten złoty prostokąt pośrodku koło – ku memu zaskoczeniu – zauważyłem, że dotyka ono stycznych do kwadratów, od których wszystko się zaczęło. To złote koło wpisało się w trójkąt o podstawie jeden i wysokości równej jeden. Odwracając to spostrzeżenie mogłem wypowiedzieć zaskakujące twierdzenie – jeżeli w trójkąt równoramienny o podstawie 1 i wysokości 1 wpisze się koło, to jego średnica będzie w złotym podziale w stosunku do podstawy (i wysokości) tego trójkąta. Nikt nigdy tego nie zauważył.
O tym, że oprócz najbardziej znanego – złotego podziału – istnieją oparte o tę samą zasadę inne podziały – nazwano je srebrnymi – dowiedziałem się od Jay Kappraffa (właściwie powinno się poprawnie mówić, że istnieje nieskończona liczba srebrnych podziałów, a pierwszy z nich nazywamy złotym).
Jak są ze sobą głęboko powiązane widać szczególnie w ułamku łańcuchowym. Nie będziemy w sam ułamek za bardzo wnikać, ale pokażemy jego piękną i wizualną moc. Kiedy oznaczamy srebrną liczbę przez – Sn, a liczbę porządkową przez – n, wtedy ogólny ułamek łańcuchowy dla wszystkich srebrnych podziałów będzie wyglądał jak poniżej.
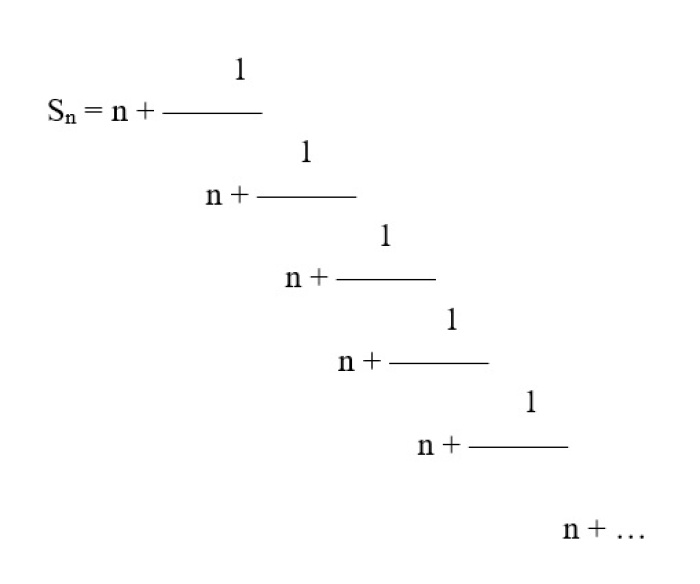
Kiedy teraz pod n wstawimy liczbę 1 otrzymamy pierwszą liczbę 1.618, czyli złoty podział.
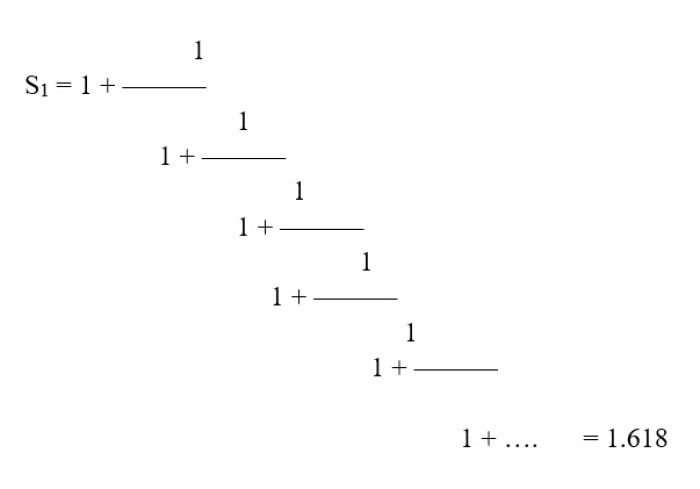
Przy n = 2 pojawia się następna srebrna liczba 2.4142
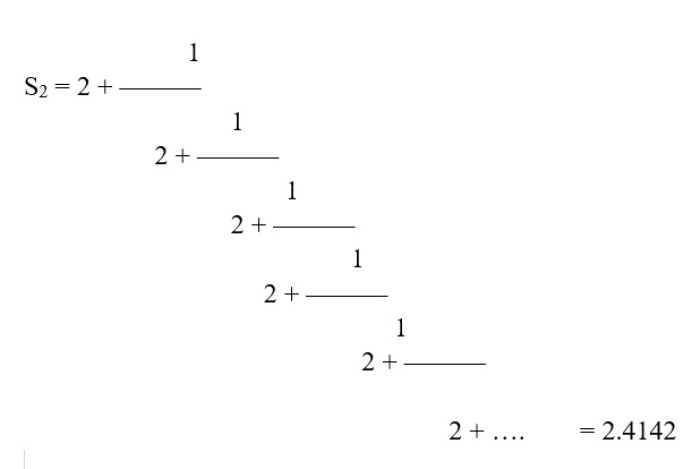
Oczywiście podmieniając kolejne liczby całkowite można je – srebrne liczby – produkować w nieskończoność. Co jest wstrząsające w ułamku łańcuchowym, a szczególnie przedstawiającym złoty podział, że składa się on tylko z liczby jeden. Jedność w relacji ze Sobą zmierza w nieskończoności do Złotej liczby! Szokujące.
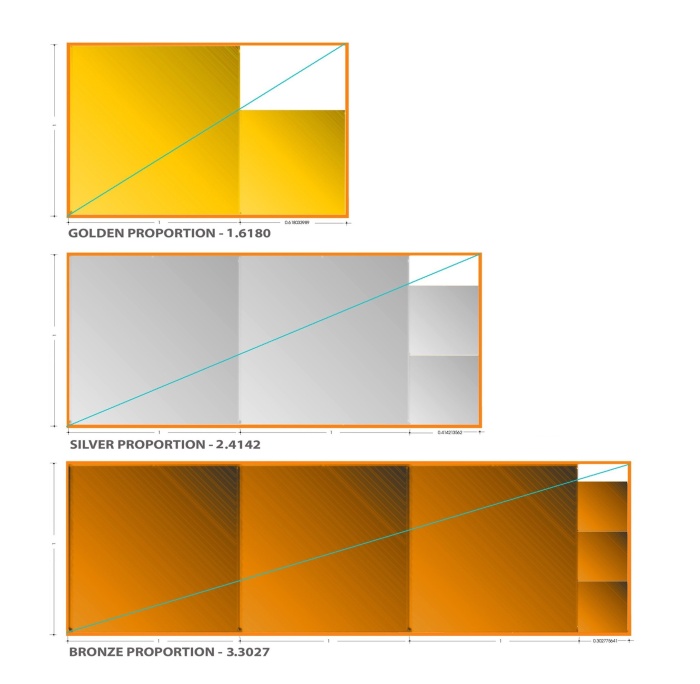
Innym, wizualnym sposobem pokazania zasady srebrnych podziałów jest ich związek z kwadratami. Jeżeli w pierwszym z kolejności srebrnych podziałów – złotym prostokącie – odetniemy kwadrat część odcięta znowu jest złotym prostokątem (rys. 14).
rys. 14
W drugim srebrnym prostokącie musimy odciąć dwa kwadraty, żeby uzyskać pomniejszony srebrny prostokąt. Itd. Tak tylko, dla przypomnienia – fasada Akropolu jest w złotym podziale, fasada Watykanu – w srebrnym.
Kiedy świadom istnienia srebrnych podziałów po spotkaniu z profesorem Kappraffem wróciłem do domu, chciałam sprawdzić pewne dziwne podejrzenie. Jak pamiętacie, kiedy w trójkąt o podstawie jeden i wysokości jeden wpisać koło – będzie ono złotym kołem. Co się stanie – i to było to moje podejrzenie – kiedy wpiszemy koło w trójkąt o podstawie 1 i o wysokości 1/2 (jedna druga)? Tak. To była moja „eureka” – koło wpisane w trójkąt wyznaczało srebrny podział! (rys. 15)
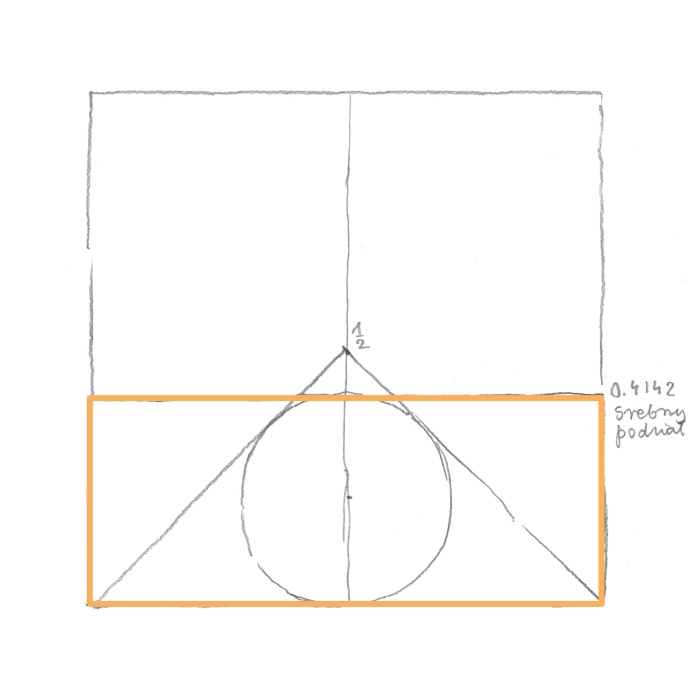
rys. 15
Do tej pory, żeby narysować złoty i srebrny podział konieczne było robienie to za pomocą dwóch różnych rysunków. Po raz pierwszy w historii udało mi się stworzyć konstrukcję/strukturę/mechanizm, który łączył je razem i ukazywał ich nieznane wcześniej relacje (rys. 16).
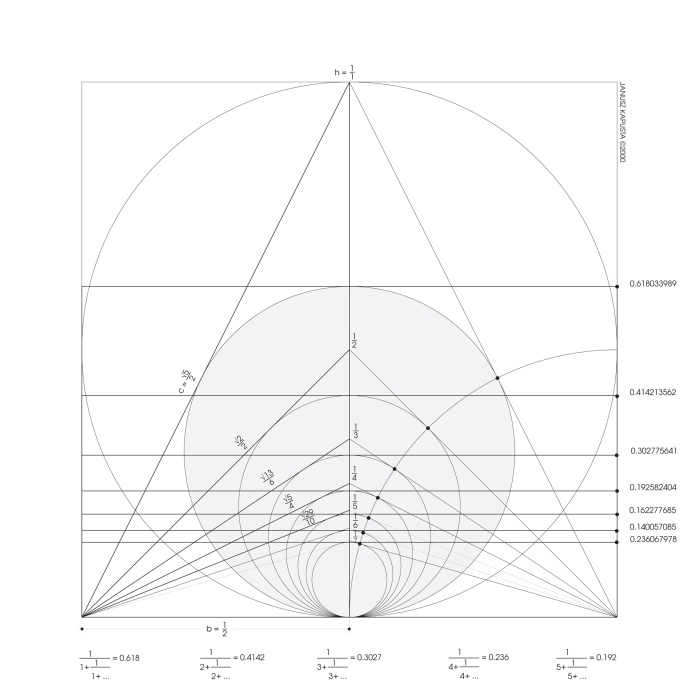
rys. 16
To wtedy prof. Jay Kappraff zaprosił mnie do napisania artykułu w „Formie”. Pojawiły się następne odkrycia. Przekonywały, że nie tylko się nie myliłem, ale że nagle zacząłem osobne wcześniej wydarzenia łączyć w jeden ciąg.
TRZECIE ODKRYCIE – KONKLUZJE
Moje odkrycia pokazały, że złota proporcja jest unikalna i złożona, i że kiedy jest postrzegana jako PIERWSZA w nieskończonej sekwencji proporcji, wyłania się jako fundamentalna relacja w konstrukcji Wszechświata. Złota proporcja nie jest już odizolowaną wyspą piękna. Ponieważ jest PIERWSZA, i z powodu jej intymnego związku z liczbą Jeden, złoty środek odciska znaczące piętno na kosmicznym zachowaniu.
Złoty podział – jak plemnik, który pomimo konkurencji milionów w biegu do komórki wygrał, był pierwszy – odciska swoje piętno na wszystkim. Na świecie, kosmosie, przyrodzie – i tak – też na myśleniu i odczuwaniu człowieka. Ludzie są bardzo różni, a przecież każdy jest człowiekiem, każdy posiada ten wspólne wszystkim ludziom kod, algorytm, liczbę. Grawitacji nie musimy się uczyć. Podobnie złotego podziału. One w nas są.
Żeby przekonać – najpierw siebie – że jest w tym jakiś sens, zacząłem badać kultury pierwotne, prymitywne, ludowe. Byłem świadom, że na pewno nic nie wiedziały o złotym podziale. Świadomie. A podświadomie?
Jeżeli, jak to wychodziło z konstrukcji, złoty podział jest matrycą, archetypem w sensie Jungowskim (archetypy – elementy strukturalny nieświadomości zbiorowej, wspólne wszystkim ludziom na świecie) musiały złoty podział odzwierciedlać. Tak – ludy Ameryki, Afryki, Azji i Europy nie wiedząc nic o złotym podziale zawsze go w swoich aktach związanych z pięknem – ujawniały. Jeżeli nie wierzycie – możecie to sprawdzić sami. Na zakończenie chcę zaprezentować tylko jeden przykład. Wykorzystam malarza z Polski. Na pewno nic o złotym podziale nie wiedział. Nazywał się Nikifor. (rys. 17)

rys. 17
W sądzie przy bardzo skomplikowane sprawie powstaje ogromna ilość dokumentacji. Dziesiątki, setki, tysiące stron. Wszystko po to, żeby sędzia/czytelnik – bazując na tych dowodach – powiedział tylko jedno słowo: winny lub niewinny. Nie wiem, czy ten stosunkowo krótki tekst pozwoli czytającemu podjąć jakąś „winną–niewinną” decyzję. Chcę tylko zapewnić, że w książce, którą przygotowuję dokumentacja będzie bardziej pełna, szersza, głębsza i zadziwiająca. Ale nie inna.
Tam też w konkluzji wyniknie, że Piękno nie jest jakimś wydumanym przez intelektualistów i artystów pojęciem, ale fundamentem Wszechświata. Jak Dobro i Prawda.
Piękno to jedyna twarz Boga, której nie udało się ukryć
Janusz Kapusta, Plus Minus, Podręcznik do myślenia, Zysk i S-ka, 2014
Rysunek: Ignacy Czwartos
Wpis jest kopią na prawach cytatu i pochodzi z serwisu Obieg.pl z artykułu znajdującego się pod adresem https://obieg.pl/218-boska-proporcja-trzecie-odkrycie
