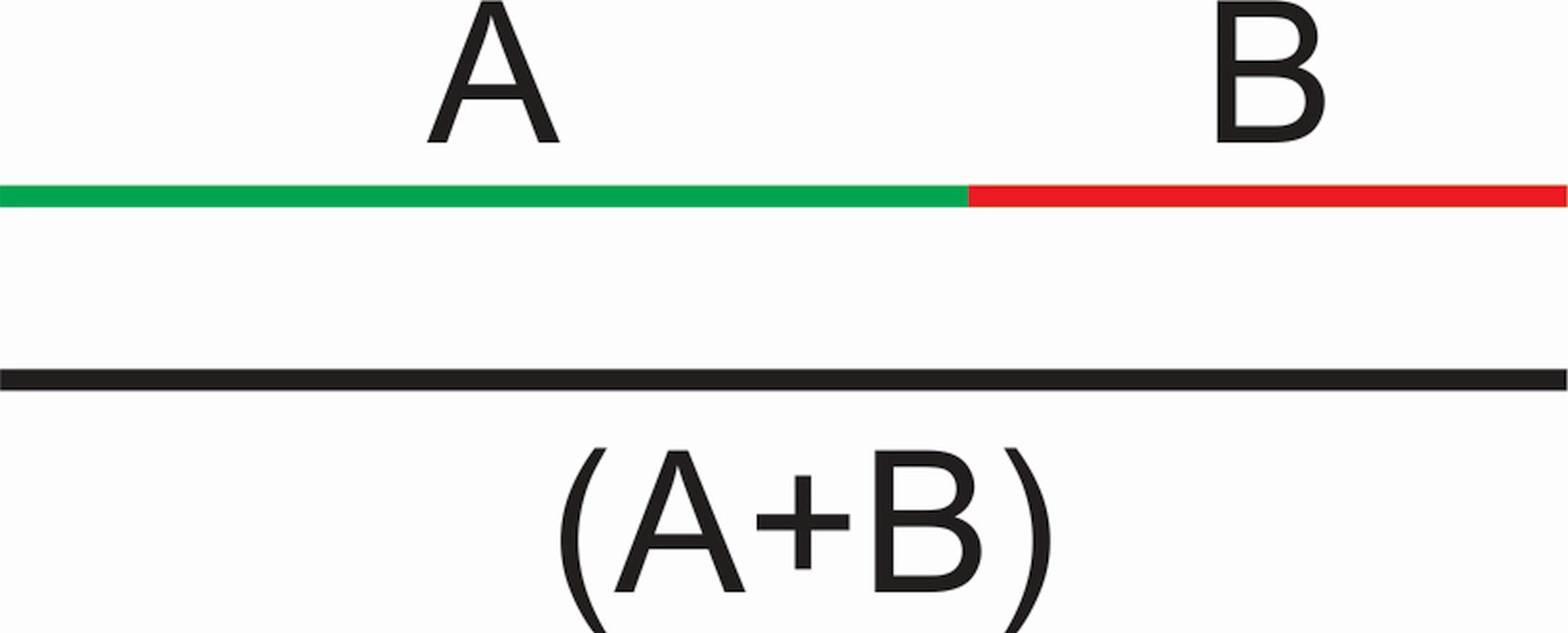
Złoty podział opisuje podział odcinka na dwie części w taki sposób, by stosunek długości dłuższej części do krótszej był równy stosunkowi całego odcinka do dłuższej jego części. Stosunek, o którym mowa w definicji, nazywa się złotą liczbą, a oznaczany grecką literą φ (czyt. fi).
Ważne daty
447–432 p.n.e. – Fidiasz tworzy Partenon, starożytną świątynię zachowującą złote proporcje
1202 – Fibonacci opisuje serię liczb nazywaną dziś Ciągiem Fibonacciego
ok. 1490 – powstaje rysunek autorstwa Leonarda da Vinci Człowiek witruwiański
1835 – Martin Ohm jako pierwszy do opisu kanonu estetycznego używa określenia złoty podział
XX w. – Mark Barr proponuje, aby symbolem złotego podziału uczynić grecką literę φ – na cześć starożytnego artysty Fidiasza, który złoty podział zawarł w wielu swoich dziełach.
Artyści w swoich dziełach nie tylko opisują świat, ale także wpływają na uczucia i emocje odbiorcy. W tym celu starannie komponują swoje prace. Kompozycja to układ elementów zestawionych ze sobą w taki sposób, aby tworzyły określoną całość. Celem kompozycji jest osiągnięcie zamierzonego efektu plastycznego. Artysta poprzez umiejętne dobranie kolorów, kształtów, proporcji, faktur i odpowiednie rozłożenie ich na płaszczyźnie lub w przestrzeni realizuje założenia artystyczne. Jednym z najważniejszych jest osiągnięcie piękna doskonałego, harmonicznego, w którym wszystkie elementy tak współgrają ze sobą, że tworzą kompozycję idealną. W tym celu od lat poszukiwano kanonu, modułu, których zastosowanie pozwala na tworzenie właśnie takich dzieł.
Zapamiętaj!
Najbardziej znanym kanonem estetycznym, wyznaczonym i opisanym już w starożytności, jest złoty podział. Ponieważ zasada ta wywodzi się bezpośrednio z obserwacji budowy systemu całego wszechświata i, jak dowodzą badania naukowe, stanowi podstawę jego harmonicznej budowy, określa się ją jako boską proporcję: sectio aurea, divina proportio.
Złoty podział opisuje podział odcinka na dwie części w taki sposób, by stosunek długości dłuższej części do krótszej był równy stosunkowi całego odcinka do dłuższej jego części. Stosunek, o którym mowa w definicji, nazywa się złotą liczbą, a oznaczany grecką literą φ (czyt. fi). Jej wartość wynosi 1,618…
Rys 1
Rys 2

Ważne!
Złoty podział wpisany jest również w proporcje ludzkiego ciała. Liczbę φ o przybliżonej wartości 1,618 u proporcjonalnie zbudowanego człowieka uzyskamy, dzieląc:
- wzrost człowieka przez odległość od stóp do pępka;
- długość nogi przez odległość od stóp do kolana;
- odległość od ramienia do końców palców przez odległość od łokcia do końców palców;
- wysokość twarzy przez szerokość twarzy;
- odległość od brwi do ust przez długość nosa.
Złoty podział według Leonardo da Vinciego
Klikając na ilustrację interaktywną, zobaczysz, jak złote proporcje w ciele człowieka przedstawił Leonardo da Vinci.

Leonardo da Vinci, „Człowiek witruwiański”, 1490, rysunek piórkiem, atramentem i ołówkiem na papierze, Gallerie dell’Accademia, Wenecja, Włochy, wikimedia.org, Domena publiczna
Zapoznaj się z fragmentem książki Kod Leonarda da Vinci Dana Browna. Główny bohater – Langdon tak tłumaczył swoim słuchaczom istotę liczby φ.
[…] – Zmierzcie odległość między ramieniem a czubkiem palców, a potem podzielcie przez odległość między łokciem a czubkiem palców. Znowu fi. Dać wam jeszcze jeden przykład? Od biodra do podłogi podzielone przez odległość od kolana do podłogi. Jeszcze raz fi. Stawy dłoni. Palce u nóg. Odległość między kręgami. Fi, fi, fi. Przyjaciele, każdy z was jest żywym hołdem złożonym boskiej proporcji […].
– Przyjaciele, jak widzicie, ten chaos w otaczającym nas świecie ma swój wewnętrzny porządek. Kiedy starożytni odkryli fi, byli pewni, że natknęli się na element budulcowy, którym posługiwał się sam Bóg, konstruując świat. I właśnie dlatego czcili Matkę Naturę […].
Przez następne pół godziny Langdon pokazywał studentom slajdy dzieł Michała Anioła, Albrechta Dürera, Leonarda da Vinci i wielu innych, wykazując zamierzoną i rygorystyczną wierność wszystkich tych artystów pędzla i piórka złotej proporcji w planach kompozycyjnych. Langdon odkrywał przed nimi fi w wymiarach architektury rzymskiego Panteonu, egipskich piramid, a nawet w budynku ONZ w Nowym Jorku. Okazało się, że fi jest obecne w strukturach sonat mozartowskich, Piątej Symfonii Beethovena, jak również w kompozycjach Bartoka, Debussy’ego i Schuberta. Na liczbie fi, mówił dalej Langdon, opierał się nawet Stradivadius, aby obliczyć dokładne miejsce i położenie otworów rezonansowych w pudle swoich słynnych skrzypiec […].
Dan Brown, Kod Leonarda da Vinci, Warszawa 2006, Wydawnictwo Albatros A. Kuryłowicz & Wydawnictwo Sonia Draga, s. 111–112.
Zasada złotego podziału w sztuce starożytnej
Znanym dziełem starożytnym, które ilustruje zasadę złotego podziału, jest rzymska rzeźba pochodząca z II wieku, będąca kopią rzeźby greckiego artysty Leocharesa. Klikając na ilustrację interaktywną, zobaczysz, w jaki sposób artysta odniósł się do kanonu złotego podziału.

Autor nieznany, „Apollo Belwederski”, II w., rzymska kopia rzeźby Leocharesa z IV w. p.n.e., Muzea Watykańskie, Watykan, wikimedia.org, Domena publiczna
W ten sposób otrzymujemy przykładowe proporcje: AU/IU = IU/IO = AI/EI = 1,618…
Na ilustracji widoczny jest między innymi:
- podział odcinka między pępkiem a stopą (IU) według złotego podziału: IO/OU = IU/IO;
- podział odcinka między czubkiem głowy a górną częścią tułowia (AI) według złotego podziału: EI/AE = AI/EI.
Polecenie 1
Przyjrzyj się ponownie rzeźbie Leocharesa, a następnie, rozwiązując ćwiczenia, wyznacz proporcje według złotego podziału dla wysokości człowieka. Pamiętaj, że pępek w tym przypadku jest punktem dzielącym odcinek odpowiadający wysokości człowieka na dwie części tak, by stosunek długości dłuższej części do krótszej wynosił φ.

Złoty podział – kompozycja
Przyjrzyj się ilustracjom zamieszczonym poniżej. Dowiesz się, jaki schemat kompozycyjny przedstawia, a także która uwzględnia złoty podział.

Ilustracja przedstawia kompozycję asymetryczną, której brak równowagi. Ukazuje dwa jabłka obok siebie i maliny. Jedno jabłko jest czerwone, drugie, znajdujące się za nim – zielone. Przy jabłkach leży pięć malin. Owoce znajdują się na poziomie środkowej wysokości obrazu i po jego lewej stronie. Tło podzielone jest na dwie części: górną niebieską i dolną żółtą. Żółta zajmuje większą część. Na ilustracji zostały wyrysowane dwa, przecinające się pod kątem prostym odcinki. Punkt przecięcia usytuowany jest na czerwonym jabłku. Na ilustracji umieszczony jest interaktywny punkt z informacją: Punkt 1: Kompozycja asymetryczna, której brak równowagi.

Kompozycja asymetryczna, której brak równowagi, online-skills, CC BY 3.0
Ilustracja interaktywna przedstawia kompozycję opartą na złotym podziale. Ukazuje dwa jabłka obok siebie i maliny. Jedno jabłko jest czerwone, drugie, znajdujące się za nim – zielone. Przy jabłkach leży pięć malin. Owoce znajdują się na poziomie środkowej wysokości obrazu, pomiędzy środkiem, a lewą krawędzią. Tło podzielone jest na dwie części: górną niebieską i dolną żółtą. Żółta zajmuje większą część. Na ilustracji zostały wyrysowane dwa, przecinające się pod kątem prostym odcinki. Punkt przecięcia usytuowany jest na czerwonym jabłku. Na ilustracji umieszczony jest interaktywny punkt z informacją: Punkt 1: Kompozycja oparta na złotym podziale. Główny motyw umieszczony w złotym punkcie.
Kompozycja oparta na złotym podziale. Główny motyw umieszczony w złotym punkcie, online-skills, CC BY 3.0Ilustracja interaktywna przedstawia kompozycję centralną. Ukazuje dwa jabłka obok siebie i maliny. Jedno jabłko jest czerwone, drugie, znajdujące się za nim – zielone. Przy jabłkach leży pięć malin. Owoce znajdują się w centrum ilustracji. Tło podzielone jest na dwie części: górną niebieską i dolną żółtą. Żółta zajmuje większą część. Na ilustracji zostały wyrysowane dwa, przecinające się pod kątem prostym odcinki. Punkt przecięcia usytuowany jest na czerwonym jabłku. Na ilustracji umieszczony jest interaktywny punkt z informacją: Punkt 1: Kompozycja centralna, główny motyw umieszczony jest w środkowej części płaszczyzny.

Kompozycja centralna, główny motyw umieszczony jest w środkowej części płaszczyzny, online-skills, CC BY 3.0
Poniżej umieszczono zdjęcie budynku będącego Siedzibą Główną ONZ w Nowym Jorku. Przyjrzyj mu się, a następnie rozwiąż ćwiczenie.

Porównaj zdjęcie całego budynku i jego górny segment ze schematami prostokąta opartego na złotym podziale, a następnie określ niżej zamieszczone zadania jako prawdziwe lub fałszywe.

Źródło: online-skills.
Ciąg Fibonacciego
Ważne!
Własności złotego podziału są blisko powiązane z Ciągiem Fibonacciego. W ciągu tym pierwsza liczba jest równa 0, druga równa 1, a każda następna jest sumą dwóch poprzednich.
Ciąg Fibonacciego zapisuje się następująco:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…,
bo
0 + 1 = 1; 1 + 1 = 2; 2 + 1 = 3; 3 + 2 = 5; 5 + 3 = 8 itd.
Jeżeli podzielimy przez siebie dowolne, kolejne dwie liczby Ciągu Fibonacciego (przy czym liczba z Ciągu Fibonacciego jest dzielona przez swojego bezpośredniego poprzednika w ciągu), to stosunek tych liczb będzie w przybliżeniu równy tej samej liczbie (około 1,618). A więc liczbie φ. Im większe liczby w ciągu podzielimy, tym uzyskamy dokładniejsze przybliżenie liczby φ.
Można wyznaczyć proporcje wynikające z ułożenia sąsiednich liczb w ciągu: 3/2 = 5/3 = 8/5 = 13/8 = 21/13 itd., które odpowiadają złotemu podziałowi.
Na zdjęciu poniżej przedstawiono przykłady liczby z Ciągu Fibonacciego w płatkach kwiatów. Przykładowo lilie i irysy mają po 3 płatki, jaskry i dzikie róże po 5 płatków, ostróżki 8 płatków, złocień polny 13 płatków, astry 21, a stokrotki po 34, 55 i 89.

Z Ciągu Fibonacciego można wykreślić złoty prostokąt, który jako jedyny ma taką właściwość, że można podzielić go (za pomocą kwadratów) na mniejsze prostokąty. W każdym z otrzymanych prostokątów również odnajdziemy złotą proporcję φ.

Złoty podział w sztukach plastycznych
Najbardziej znanym starożytnym artystą stosującym złoty podział był grecki rzeźbiarz Fidiasz. To jeden z twórców Świątyni Ateny Partenon zbudowanej na Akropolu w Atenach, która jest zaprojektowana według złotego podziału. Widoczne jest to zarówno w planie świątyni, jak również w proporcjach całego jej układu, np. w odległości pomiędzy kolumnami, w wielkości fryzu i znajdujących się tam tryglifach. Na zdjęciu zamieszczonym niżej możesz zobaczyć, jak współcześnie wygląda ta świątynia. Po kliknięciu w zdjęcie zobaczysz, jak fronton świątyni wpisuje się w złoty prostokąt (w czasach, kiedy jego trójkątne zwieńczenie nie było jeszcze zniszczone).Ilustracja interaktywna przedstawia ruiny świątyni Ateny. Ateńska świątynia znajduje się na wzgórzu. Fragment przyczółku wsparty jest na ośmiu kolumnach w stylu doryckim, nad którymi znajduje się przyczółek. Fryz zdobią tryglify i metopy. Przed budowlą znajduje się kamienisty teren. po którym chodzą turyści. Na ilustracji umieszczony jest interaktywny punkt z ilustracją przedstawiającą tę samą świątynię, ale z wyrysowanym cienką czerwoną linią konturem opisanego na niej prostokąta. Przerywaną linią oznaczono brakującą część tympanonu. Podziały czerwonymi liniami wprowadzone zostały także we fryzie.
Świątynia Ateny w Atenach, online-skills, CC BY 3.0
Zapamiętaj!
Zasadę złotego podziału w sztukach plastycznych można stosować na wiele sposobów.
Przykładowo może ona być podstawą do:
- wyznaczenia wymiarów podłoża, płaszczyzny tworzonego dzieła (stosunku długości jego boków);
- rozmieszczenia elementów dzieła;
- wyznaczenia proporcji każdego elementu kompozycji.
Kompozycja oparta na złotym podziale jest harmoniczna i równoważna, przez co staje się przyjemna do oglądania. Zasada ta powszechnie była stosowana w starożytności, w sztuce renesansu, sztuce klasycyzmu, a także w wybranych dziełach sztuki współczesnej. Do najbardziej znanych artystów, którzy w swoich kompozycjach odwoływali się do zasady złotego podziału, należeli np.: Leonardo da Vinci, Sandro Botticelli, Piero della Francesca, Nicolas Poussin czy Salvador Dali.
Kliknij, aby uruchomić podgląd
Slajd 1 z 5

Złota spirala
Z podziału złotego prostokąta możemy wyprowadzić złotą spiralę. W każdy z kwadratów odciętych od poszczególnych złotych prostokątów należy wrysować ćwiartkę okręgu w taki sposób, aby płynnie przechodzić od najmniejszego kwadratu do kolejnych. Schemat złotej spirali przedstawiony jest na ilustracji umieszczonej niżej.

Złotą spiralę można spotkać w całym wszechświecie. Przykładowo, spiralny kształt muszli łodzika (Nautilus pompilius) czy małżowiny usznej, rozszerza się zgodnie z zasadą proporcji φ.
Rys 1


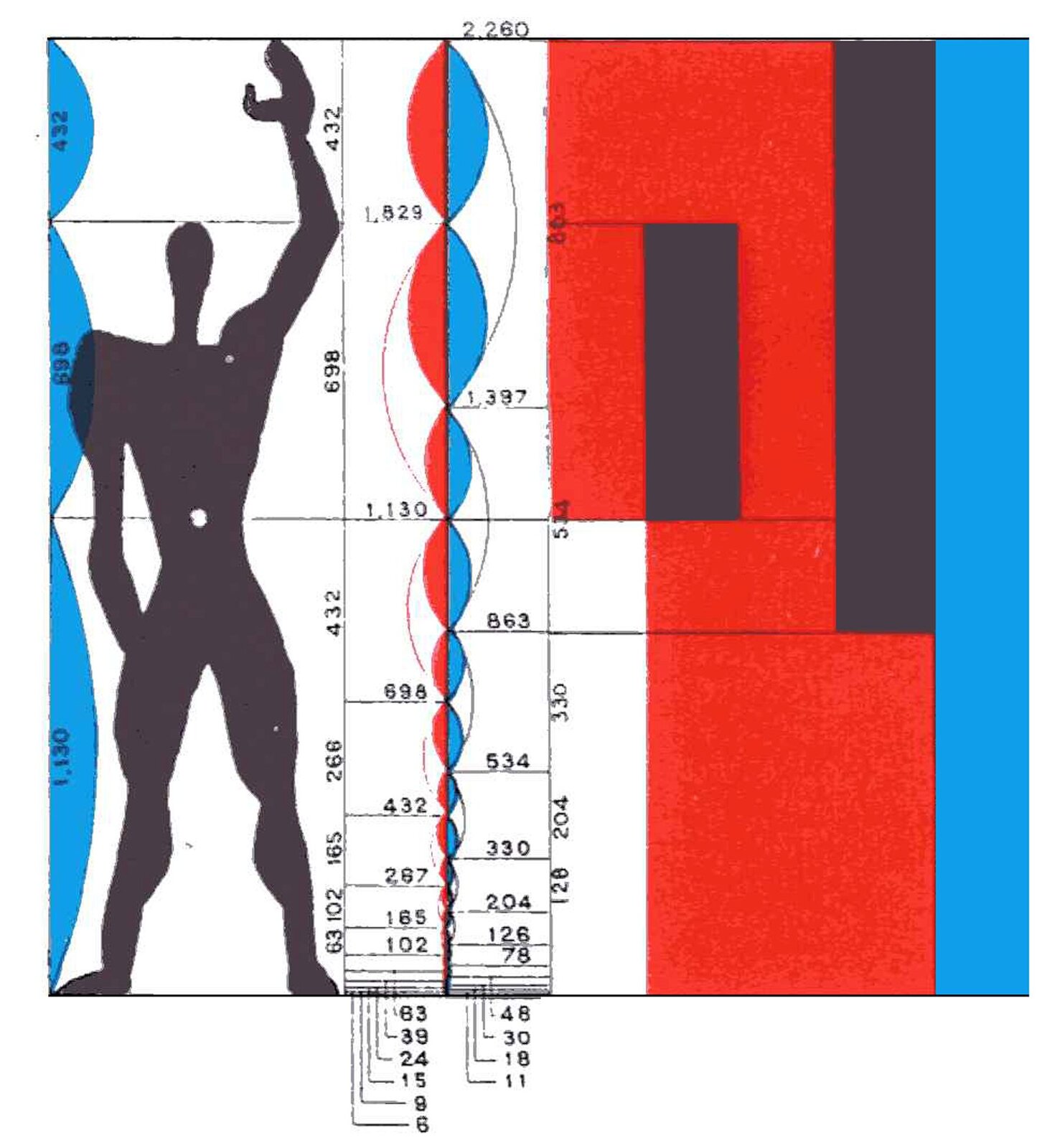
Złoty podział wykorzystywany jest w architekturze, sztuce, fotografii, projektowaniu, ale także w ekonomii i marketingu. Słynny artysta pierwszej połowy XX wieku – Le Corbusier, całą swoją twórczość architektoniczną oparł na zasadzie złotego podziału. Opracował według tej zasady system podziałów, proporcji stosowany do określania relacji między wielkościami poszczególnych elementów budowli. Podstawą obliczeń była umowna postać stojącego człowieka mierzącego 183 cm (kolor czerwony) i z podniesioną ręką mierzącego 226 cm (kolor niebieski).
Zobacz schemat według złotego podziału opracowany przez Le Corbusiera.
Przyjrzyj się dziełom architektonicznym Le Corbusiera, w których wykorzystywana jest zasada złotego podziału.
Kliknij, aby uruchomić podgląd
Slajd 1

Slajd 2

Slajd 3

Słownik pojęć
Fryz
W budowlach klasycznych: środkowa część belkowania między architrawem a gzymsem.
Kanon
Reguła kompozycyjna, której podstawą jest nauka o proporcjach określających stosunki wszystkich części do siebie i całości. Kanon także określa idealne proporcje wyobrażonego ciała ludzkiego.
Leonardo Fibonacci
Zwany Leonardem z Pizy, włoski matematyk, który w 1202 roku opracował ciąg liczb noszący nazwę Ciągu Fibonacciego. Jest to specyficzny ciąg liczb naturalnych, w którym każdy kolejny wyraz stanowi sumę dwóch poprzednich.
Moduł
Najsłuszniejsza, powtarzalna wielkość elementu głównego w stosunku do całości kompozycji. Moduł stanowić może nie tylko o proporcjach człowieka, ale wszystkich jakościach plastycznych, jak np. wielkości plamy barwnej, stopniu zagęszczenia faktury, jasności światła itp.
Tryglif
Prostokątna płyta z trzema ostrymi pionowymi żłobkami, umieszczona pomiędzy metopami i w narożach fryzu belkowania doryckiego, imitująca zbite razem ze sobą trzy deski wewnętrznego belkowania.
Źródło: sjp.pwn.pl
Źródło wpisu: https://zpe.gov.pl/a/boskie-proporcje—zloty-podzial/DTnOU1Djn

Ten blog to niczym otwarta przestrzeń dla myśli, gdzie każdy artykuł to jak nowa kraina do odkrycia, a autor to jak doświadczony pionier, który otwiera przed nami drzwi do nieznanych obszarów wiedzy.
Pouczająca lektura! Doceniam szczegółowość i dokładność. Szkoda tylko, że niektóre fragmenty są zbyt techniczne dla laików. Mimo to, świetne źródło wiedzy!